
An infinite distance: stars in the sky
Since the time of the Sumerians, about 3000 BC, scientists have studied the stars and the planets. They’ve tried to figure out the patterns in the movements of the planets. This was much harder because everybody thought that the stars and planets circled around the earth, and really they don’t. About 140 BC, the Greek astronomer Hipparchus of Rhodes still thought that the stars and planets went around the earth. But he realized that you could use a system of imaginary right triangles connecting the earth to the planet or star to calculate patterns in the planet or star’s movements. This was the beginning of trigonometry.

An Islamic astrolabe (832 AD)
Hipparchus developed trigonometry when he realized that Euclid‘s geometry couldn’t help him with the geometry of things that were moving in space. Hipparchus was looking at the movement of planets. So he needed math that would deal with moving, changing things, not just things standing still. Trigonometry is the simplest geometry that deals with moving objects. About 500 AD, the Indian mathematician Arya Bhata developed Hipparchus’ ideas further. He defined the ideas of the sine and the cosine, and wrote the first table of sines. In the 1200s AD, al-Tusi, in Iran, shifted trigonometry to being more about math and less about astronomy.
Trigonometry means the measurement of triangles, and trigonometry begins by measuring triangles. If you have a right triangle, and the hypotenuse gets longer, trigonometry lets you calculate what will happen to the angles, and to the other sides of the triangle. The main trigonometric functions are the sine, the cosine, and the tangent. You can remember how to calculate them with the mnemonic SOHCAHTOA: Sine=Opposite over Hypotenuse, Cosine = Adjacent over Hypotenuse, Tangent = Opposite over Adjacent.
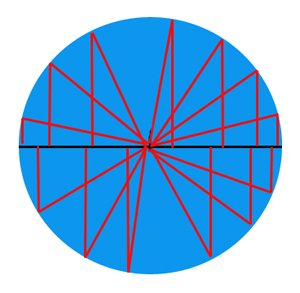
Triangles define a circle
But trigonometry’s also a way of describing circles, like the orbit of the moon around the earth. Choose a point, and draw a black line segment horizontally across it to be the diameter of your circle. Along that diameter, mark a lot of points, evenly spaced and close together. Now draw a red right triangle: one side lies along your first line, going to the mark next to the end of your diameter line. The second side of your right triangle is the hypotenuse: it’s the same length as half your diameter, but angled slightly upward. The third side of your triangle connects the other two, making a right angle with the first diameter line.
Draw more of these triangles, all of them with one side half the diameter, and the second side along the black diameter line, each to a different mark on the line. If you drew an infinite number of these triangles, touching each point on your diameter line and going both above and below your diameter line, you’d have a circle.
Hipparchus didn’t know it, but If you don’t wrap your line around into a circle, but instead keep going always in the same direction, you’ll get a repeating wave like on the right side of the video – sine waves. Sine waves are the most efficient way for a cycle to act, so lots of things in nature besides orbits cycle in sine waves. Trigonometry can help describe and predict all of these natural things. Sunlight travels with waves like this of getting stronger and weaker. Sound travels by creating cycles of more or less air pressure. Electricity, microwaves, radio waves, and ocean waves are also things we can describe using trigonometry.
Here’s a page where you can move the triangles around the circle for yourself.




