Right triangle and cosine
What is a cosine?
A cosine, like a sine, is a mathematical way of thinking about a kind of movement that happens in nature. A cosine is really just a rephrasing of the same information we already had for calculating the sine function.
What’s a sine?
More trigonometry
History of astronomy
All our math articles
Cosine changes along with the sine
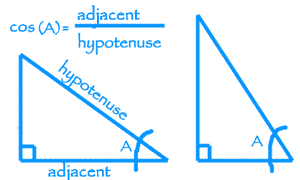
One way to describe these changes is with the sine function. Imagine a right triangle. Choose one of the two angles – A in this drawing – and divide the length of the side opposite that angle by the length of the hypotenuse. As the angle gets bigger, the opposite side will get longer. The sine will get bigger. But a second way is with the cosine function. Instead of dividing the opposite side by the hypotenuse, the cosine divides the adjacent side by the hypotenuse. As with sines, if you change the lengths of the sides of the triangle, the cosine changes along with the sine.
More about triangles
What is a right triangle?
Cosine and sine move in opposite directions
The cosine wave and the sine wave for the same natural phenomenon go up and down by the same amount, but out of phase: the cosine reaches the bottom of the wave when the sine is at zero, and the sine reaches the bottom of the wave when the cosine is at zero.
Why are cosines useful?
Cosines are useful mainly because they let people work out how far away something is just by knowing the angle near them and the length of the hypotenuse, or work out the size of an angle by knowing the length of two sides. Early astronomers like Hipparchus in Greece and Ptolemy in Egypt used cosines to help figure out the movements of the planets through space.
Hipparchus and trigonometry
Who was Ptolemy?
African math and science
All our Africa articles
Cosines, light waves, and sound waves
Later on, scientists realized that cosines are also useful for measuring and predicting how waves will behave: not ocean waves, but sound waves and light waves. These waves are like an infinite number of these triangles, growing and shrinking, growing and shrinking, over and over again. Working with these waves brought us radio, then television, then fiber optic cable and the Internet.




