
Proof of the circumference of a circle
Will this formula work every single time?
Proving that the formula for the circumference of a circle is always true is harder than just figuring out that it is true. Now we need to show that C=2πr is always true for every possible circle.
Definition of a circle
Circumference of a circle
All our math articles
How Archimedes proved it
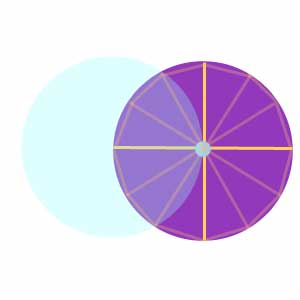
Here is how Archimedes proved it. Draw any circle. Make a point anywhere on the circumference of the purple circle. Use that point as the center of a blue circle with the same radius as the purple circle. The edge of the blue circle should touch the center of the purple circle.
Who was Archimedes?
Greek math and geometry
Egyptian math and science
Make two equilateral triangles
Draw the line segment connecting the centers of the two circles. That’s the radius of the both circles. Now draw the line connecting the center of the blue circle to where it crosses the purple circle on both sides, and complete the triangles. You should have two equilateral triangles whose sides are equal to the radius of the purple circle.
Equilateral triangles
What’s a radius?
What’s a line segment?
More of the proof
Make a hexagon
Now extend all of the radius lines so they become diameter lines, all the way across the circle, and finish drawing all of the triangles to connect them. You’ve got six equilateral triangles now, that make an orange hexagon. So the perimeter of your hexagon is the same as six times the radius of your circle.
What’s a diameter?
What’s a hexagon?
What’s the perimeter?
(Now pi comes into it)
But your circumference is a little bigger than the perimeter of your hexagon, because the shortest distance between two points is always a straight line. This shows you that the circumference of the purple circle has to be more than 6r, so if C=2πr then π (pi) has to be a little bigger than 3, which it is.
What is pi?
Drawing a dodecagon
Now let’s try to get a little closer to the real value of π. Suppose we make our triangles narrower, so that instead of drawing a hexagon, we draw a dodecagon – a shape with twelve sides? We can do that by drawing more points halfway between the points of the hexagon.
If we do that, we’ll see that that the perimeter of the dodecagon is a little bigger, and closer to being a circle. We have twelve congruent isosceles triangles. Each triangle has two sides that are as long as the radius of the circle, and a third side that we want to know the length of, in order to figure out the perimeter of the dodecagon.
What’s an isoceles triangle?
Getting the hexagon to be more like a circle
Perimeter of a dodecagon
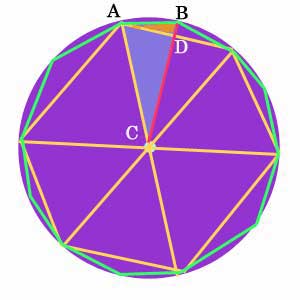
It’s pretty hard to figure out the perimeter of the dodecagon. Start by drawing a red line from the center of the purple circle to one of the points of the dodecagon (B).
We know that the line AC is the same as the radius of the circle – let’s say the radius is 4. It’s also the hypotenuse of the bluish right triangle ADC.
What’s a hypotenuse?
What’s the Pythagorean theorem?
We also know that the line AD is the same as half the radius of the circle (remember the hexagon was made of equilateral triangles), so AD = 2. Because the bluish triangle is a right triangle, we can use the Pythagorean Theorem to tell us that the third side, CD, is the square root of 12. (4 squared = 2 squared + 12).
Or you can get the same proof from this video
Stay with me…
We also know that the red line CB is the same as the radius of the circle, so that’s also 4. So the distance from point B to point D must be the radius (4) minus the length of CD, or the square root of 12. BD = 4 – the square root of 12. Now look at the little orange triangle ABD. That’s also a right triangle, and now we know two of its sides. AD = 2, and BD = 4 – the square root of 12.
We can use the Pythagorean Theorem again to calculate that the green line AB must be 2.07, so the whole perimeter is 12 x 2.07 = 24.84. The circumference of the purple circle has to be more than 24.72, or more than 6.21 r. If C = 2πr, then π has to be a little bigger than 3.1.
The more sides, the closer to pi
The more sides we draw on our polygon, the closer we will get to the real value of pi (3.14159 etc.). Using a polygon with 96 sides, Archimedes was able to calculate that π was a little bigger than 3.1408, which is pretty close.
More about circles
More about Geometry
Bibliography and further reading about geometry: