A right triangle.
This is the proof of the Pythagorean Theorem supposedly written by Pythagoras about 500 BC:
The Pythagorean Theorem says that in a right triangle, the sum of the squares of the two right-angle sides will always be the same as the square of the hypotenuse (the long side). A2 + B2 = C2. Try it yourself: if Side A is 4 inches long, and Side B is 3 inches long, then 4×4=16, and 3×3=9, and 9+16=25, and so Side C will be 5 inches long. Try it with other size triangles and see if this is still true (you can use a calculator, or your computer, to figure out the square roots).
But how can you know that this is always true, every single time, no matter what size the triangle is?
Take a straight line and divide it into two pieces, and call one piece a and the other piece b, like this:
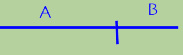
Now make a square with this line on each side, like this:
and draw in the lines where A meets B on each side to make four smaller shapes.
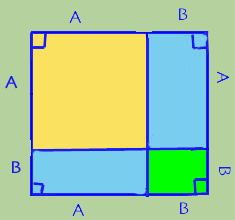
So now you have one square with area AxA (the big yellow one) and one square with area BxB (the little green one) and two rectangles with area AxB (the light blue ones). So the area of the whole square is (A+B) x (A+B) or the area is (AxA) + 2(AxB) + (BxB).
Or you might say that
(A+B)2 = A2 + 2AB + B2
Now draw diagonal lines across the blue rectangles, making four smaller blue triangles. Call those lines C. Do you see that you have made four blue right triangles, whose sides are A, B, and C?
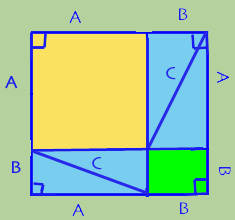Now imagine that you take these triangles and rearrange them (or if you print it out you can cut them up with scissors and really rearrange them) around the edges of the square like this:
The little triangles take up part of the square. The area of all four triangles together is the same as the two blue rectangles you made them from, so that is 2AB.
The area of the pink square in the middle is CxC or C2.
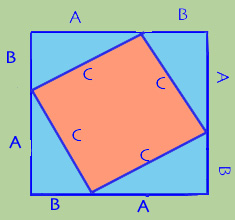
And the area of the whole big square is, as we have already seen,
A2 + 2AB + B2
So A2 + 2AB + B2 = 2AB + C2
We can subtract 2AB from both sides, so
that gives (ta da!)
A2 + B2 = C2
Learn by Doing – Proving the Pythagorean Theorem
More about Pythagoras
Bibliography and further reading about Pythagoras:
What’s Your Angle, Pythagoras? A Math Adventure, by Julie Ellis and Phyllis Hornung (2004). For teens.
Pythagoras and the Pythagoreans: A Brief History, by Charles Kahn (2001).
History of Greek Mathematics: From Aristarchus to Diophantus, by Thomas L. Heath (1921, reprinted 1981). A lot of Euclid, but also describes who the other major Greek mathematicians were and what they did.
Episodes from the Early History of Mathematics, by Asger Aaboe (1997).
.
